
- Автор Miles Stephen [email protected].
- Public 2023-12-15 23:33.
- Последно модифициран 2025-01-22 16:56.
Правилото на Декарт за знаците казва броят на положителните корени е равно на промените в знак на f(x) или е по-малко от това с четно число (така че продължавате да изваждате 2, докато не получите 1 или 0). Следователно предишното f(x) може да има 2 или 0 положителни корени . Отрицателен реален корени.
Хората също така питат какво ви казва правилото на Декарт за знаците за истинските корени на полинома?
Декарт ' правило на знак. Декарт ' правило на знака е свикнал определи броят на истински нули на a полином функция. То разказва ни, че броят на положителните истински нули в а полином функцията f(x) е същата или по-малка от четни числа като броя на промените в знака на коефициентите.
Знайте също, колко реални корени има един полином? Ако броим корени според тяхната множественост (виж Теоремата за факторите), тогава: A полином на степен n може имат само четно число, по-малко от n истински корени . Така, когато броим множественост, куб полином мога имат само три корени или един корен ; квадратична полином мога имат само две корени или нула корени.
Оттук нататък какво е истинска нула?
Истински нули . Припомнете си, че а реална нула е мястото, където графиката пресича или докосва оста x. Помислете за някои точки по оста x.
Колко корена има едно уравнение?
А квадратична уравнение с реални коефициенти може имат едно или две различни реални корени , или два различни комплекса корени . В този случай дискриминантът определя броя и естеството на корени . Има три случая: Ако дискриминантът е положителен, тогава има два различни корени.
Препоръчано:
Как намирате приблизителния процент, като използвате емпиричното правило?

Намиране на площта под кривата от x = 9 до x = 13. Емпиричното правило или правилото 68-95-99,7% дава приблизителния процент данни, които попадат в рамките на едно стандартно отклонение (68%), две стандартни отклонения (95%) и три стандартни отклонения (99,7%) от средната стойност
Как решавате правилото на Декарт за знаците?

Правилото на Декарт за знаците ни казва, че тогава имаме точно 3 реални положителни нули или по-малко, но нечетен брой нули. Следователно нашият брой положителни нули трябва да бъде или 3, или 1. Тук можем да видим, че имаме две промени на знаците, следователно имаме две отрицателни нули или по-малко, но четен брой нули
Как намирате радиуса на окръжност, като използвате пи?
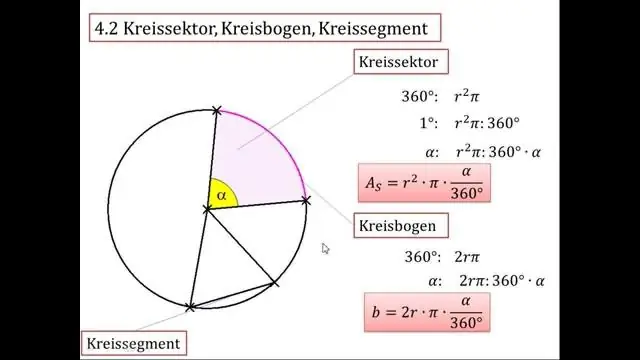
За да изчислите радиуса на окръжността, като използвате окръжността, вземете обиколката на окръжността и я разделете на 2 пъти π. За кръг с обиколка 15, ще разделите 15 на 2 по 3,14 и ще закръглите десетичната запетая до вашия отговор от приблизително 2,39
Как използвате въображаеми числа на калкулатор?
Вашият калкулатор показва само опростения отговор, както е показано на първия екран. Комплексните числа не могат да се използват с шаблона за n/d фракция. Вместо това въведете комплексни числа като дроби, като използвате скоби и клавиша за деление. Натиснете [MATH][ENTER][ENTER], за да покажете отговора на комплексното число под формата на дроби
Можете ли да използвате правилото за продукта вместо правилото за частното?

Има две причини, поради които правилото за частно може да бъде по-добро от правилото за степен плюс правилото за продукт при диференциране на частно: То запазва общите знаменатели, когато опростява резултата. Ако използвате правилото за мощност плюс правилото за продукта, често трябва да намерите общ знаменател, за да опростите резултата
