
- Автор Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Последно модифициран 2025-01-22 16:56.
В метод на черупката изчислява обема на пълното твърдо тяло на въртене чрез сумиране на обемите на тези тънки цилиндрични черупки като дебелината Δ x Delta x Δx отива до 0 0 0 в границата: V = ∫ d V = ∫ ab 2 π xydx = ∫ ab 2 π xf (x) dx. V = int dV = int_a^b 2 pi x y, dx = int_a^b 2 pi x f(x), dx.
Точно така, каква е формулата на метода на Shell?
В метод на черупката разчита на лесна геометрична формула . Много тънък цилиндричен черупка може да се апроксимира с много тънко правоъгълно твърдо тяло. По този начин обемът на черупка се апроксимира с обема на призмата, който е L x W x H = (2 π r) x h x dr = 2πrh dr.
Освен това, каква е формулата на дисковия метод? С други думи (по-малко цветни думи), the дисков метод е процесът на намиране на обема на обект чрез разделяне на този обект на много малки цилиндри/ дискове и след това добавяне на обемите на тези малки дискове заедно. Радиусът на цилиндъра е даден от функция f(x), а височината е промяната в x.
По същия начин хората питат как използвате метода на измиване в смятането?
Как да намерите обема на фигура с помощта на метода на шайбата
- Определете къде се пресичат двете криви. Така че въпросното твърдо тяло обхваща интервала по оста x от 0 до 1.
- Определете площта на шайба с напречно сечение.
- Умножете тази площ по дебелината dx, за да получите обема на представителна шайба.
- Съберете обемите на шайбите от 0 до 1 чрез интегриране.
Какъв е методът на цилиндричната обвивка?
В метод с цилиндрична обвивка . Използвай метод на черупката за да се изчисли обемът на твърдото вещество, проследено чрез завъртане на областта, ограничена от оста x, кривата y = x3 и правата x = 2 около оста y. Тук y = x3 и границите са от x = 0 до x = 2.
Препоръчано:
Как Нютон е използвал смятането?
Нютон е известен с разработването на законите на движението и гравитацията, което несъмнено е довело до работата му в смятане. Когато се опитвал да опише как пада обект, Нютон открива, че скоростта на обекта се увеличава с всяка част от секундата и че никаква математика, използвана в момента, не може да опише обекта във всеки един момент от времето
Колко орбитали има в обвивката N 4?

L=3 за f подчерупка. Броят на орбиталите е = 2l+1=7. Може да побере общо 14 електрона. Следователно за обвивка с главно квантово число n=4 има 16 орбитали, 4 подобвивки, 32 електрона (максимум) и 14 електрона с l=3
Как използвате метода за изместване на водата, за да намерите обема на неправилен обект?

Поставете обекта в градуирания цилиндър и запишете получения обем вода като „b“. Извадете обема само на водата от обема на водата плюс обекта. Например, ако "b" е 50 милилитра, а "a" е 25 милилитра, обемът на обекта с неправилна форма ще бъде 25 милилитра
Как пишете формули с помощта на метода Criss Cross?
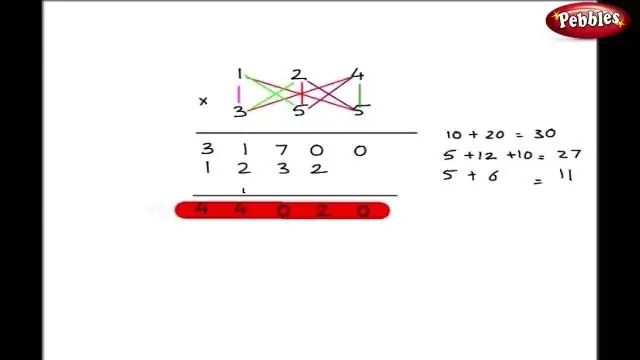
Алтернативен начин за писане на правилна формула за йонно съединение е използването на кръстосания метод. При този метод числовата стойност на всеки от йонните заряди се пресича, за да стане индекс на другия йон. Признаците на обвиненията отпадат. Напишете формулата за оловен (IV) оксид
Колко орбитали има в обвивката с n 5?

За n = 3 има девет орбитали, за n = 4 има 16 орбитали, за n = 5 има 52 = 25 орбитали и т.н
