
- Автор Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Последно модифициран 2025-01-22 16:56.
Когато се сравняват две популации, колкото по-голямо е стандартното отклонение, толкова по-голяма е дисперсията разпределението има, при условие че променливата от интерес от две популации има същия набор от мерки.
Точно така, какво е стандартното отклонение, използвано във връзка с?
В стандартно отклонение е използвани във връзка с MEAN за числено описание на разпределения, които са с форма на камбана. СРЕДНОТО измерва центъра на? разпространение, докато стандартно отклонение измерва РАЗПРОСТРАНЕНИЕТО на разпространението.
Освен това, какво е емпиричното правило в статистиката? В емпирично правило заявява, че за нормално разпределение почти всички данни ще попаднат в рамките на три стандартни отклонения на средната стойност. В емпирично правило може да се раздели на три части: 68% от данните попадат в рамките на първото стандартно отклонение от средната стойност. 95% попадат в две стандартни отклонения.
Що се отнася до това, какво е ограничението на обхвата като мярка за дисперсия?
ОБХВАТ . В обхват е разликата между най-голямото и най-малкото наблюдение в данните. Основното предимство на това мярка за дисперсия е, че е лесно да се изчисли. От друга страна, тя има много недостатъци.
Какво представлява броят на стандартните отклонения на едно наблюдение от средната стойност?
Z-резултатът често се нарича стандартизирана стойност. Z-резултатът измерва брой стандартни отклонения и наблюдение е над или под означава . напр. Z-резултат 1.24 се интерпретира като „стойността на данните е 1.24 стандартно отклонение над означава ."
Препоръчано:
Как изчислявате стандартното отклонение от PMP?

Формулата, използвана в PMBOK за стандартно отклонение, е проста. Това е просто (P-O)/6. Това е песимистичната оценка на активността минус оптимистичната оценка на активността, разделена на шест. Проблемът е, че тази форма или форма по никакъв начин не произвежда мярка за стандартно отклонение
Какво е стандартното отклонение, използвано във връзка с?
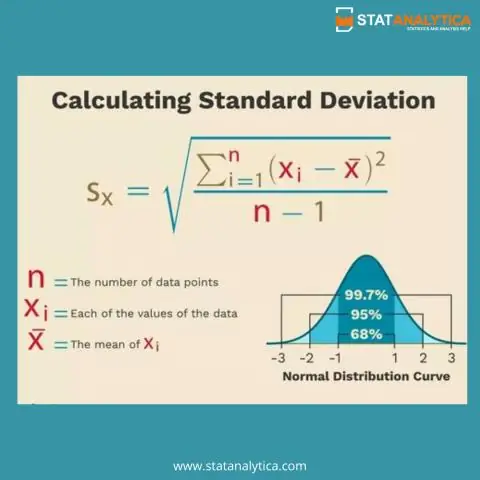
Стандартното отклонение се използва във връзка със средното значение за числено описание на разпределения, които имат форма на камбана. СРЕДНОТО измерва центъра на? разпределението, докато стандартното отклонение измерва РАЗПРОСТРАНЕНИЕТО на разпределението
Как изчислявате стандартното отклонение в SPC?

Изчисляване на стандартното отклонение Изчисляване на средната стойност на процеса μ Извадете средната стойност на процеса от всяка измерена стойност на данните (стойностите X i) Квадратирайте всяко от отклоненията, изчислени в стъпка 2. Съберете всички квадратни отклонения, изчислени в стъпка 3. Разделете резултата от стъпка 4 от размера на извадката
Как намирате стандартното отклонение и средната стойност в Excel?
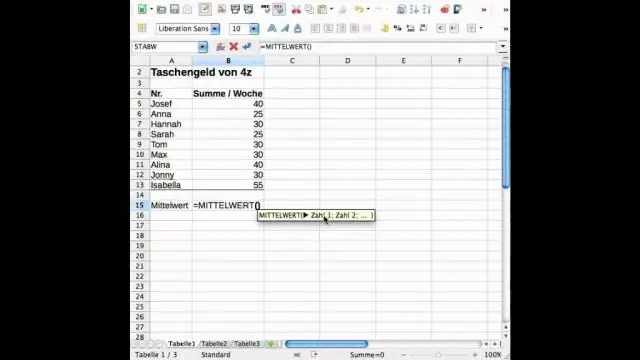
Стандартното отклонение е мярка за това колко дисперсия има в набор от числа в сравнение със средната стойност (средната) на числата. За да изчислите стандартното отклонение в Excel, можете да използвате една от двете основни функции, в зависимост от набора от данни. Ако данните представляват цялата популация, можете да използвате STDEV. Pфункция
Как намирате стандартното отклонение от променливостта?

За да изчислите стандартното отклонение, съберете всички точки от данни и ги разделете на броя на точките от данни, изчислете дисперсията за всяка точка от данни и след това намерете квадратния корен от дисперсията
