
Съдържание:
- Автор Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Последно модифициран 2025-01-22 16:56.
Процес за графиране на рационална функция
- Намерете прихващанията, ако има такива.
- Намерете вертикалните асимптоти, като зададете знаменателя равен на нула и решите.
- Намерете хоризонталната асимптота, ако съществува, като използвате факта по-горе.
- Вертикалните асимптоти ще разделят числовата права на области.
- Скицирайте графика .
По същия начин се пита как се изобразява графика на най-тежката рационална функция?
Как да изобразяваме рационални функции от уравнения в 7 лесни стъпки
- Вижте дали има дупки.
- Намерете ВЕРТИКАЛНИ АСИМПТОТИ, като откриете къде факторите в знаменателя са равни на нула.
- Вижте дали фракцията е ГОРЕ ТЕЖКА, ДОЛНА ТЕЖКА ИЛИ БАЛАНСИРАНА за невертикални (хоризонтални и наклонени/наклонени) асимптоти.
- Намерете пресечките на x, където числителят е равен на нула.
Знайте също, как определяте асимптотите? mpto?t/) на крива е такава, че разстоянието между кривата и правата се доближава до нула, тъй като една или и двете координати x или y клонят към безкрайност.
Имайки предвид това, какво прави една функция рационална?
В математиката, а рационална функция е всякакъв функция който може да бъде дефиниран от a рационално дроб, т.е. алгебрична дроб, такава че и числителят, и знаменателят са полиноми. Коефициентите на полиномите не трябва да бъдат рационално числа; те могат да бъдат взети във всяко поле K.
Как се пише уравнение за асимптота?
като следвате тези стъпки:
- Намерете наклона на асимптотите. Хиперболата е вертикална, така че наклонът на асимптотите е равен.
- Използвайте наклона от стъпка 1 и центъра на хиперболата като точка, за да намерите формата точка-наклон на уравнението.
- Решете за y, за да намерите уравнението във формата на пресечен наклон.
Препоръчано:
Как се изобразяват графики на неравенства в координатна равнина?

Има три стъпки: Пренаредете уравнението, така че 'y' да е отляво, а всичко останало отдясно. Начертайте линията 'y=' (направете я плътна линия за y≤ или y≥ и пунктирана линия за y) Засенчвайте над линията за 'по-голямо от' (y> или y≥) или под линията за a 'по-малко от' (y< или y≤)
Как е разделянето на рационални числа като деленето на цели числа?

Просто умножете абсолютните стойности и направете отрицателен отговор. Когато разделите две цели числа с еднакъв знак, резултатът винаги е положителен. Просто разделете абсолютните стойности и направете отговора положителен. Когато разделите две цели числа с различни знаци, резултатът винаги е отрицателен
Как се изобразяват графики на котангенс?
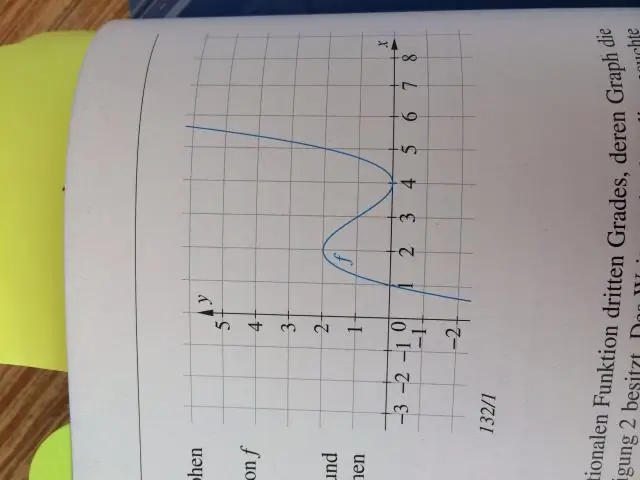
За да скицирате пълната родителска графика на котангенса, следвайте тези стъпки: Намерете вертикалните асимптоти, за да можете да намерите домейна. Намерете стойностите за диапазона. Определете x-пресеките. Оценете какво се случва с графиката между x-пресечките и асимптотите
Как се изобразяват логаритмични функции на калкулатор?

В графичния калкулатор основният е логаритъм е ключът ln. И трите са еднакви. Ако имате функцията logBASE, тя може да се използва за въвеждане на функцията (виждана в Y1 по-долу). Ако не, използвайте формулата за промяна на основата (вижте в Y2 по-долу)
Какво представляват цели числа и рационални числа Как се изобразяват точки на координатна равнина?

Както казахме, точките в координатната равнина се представят като (a, b), където a и b са рационални числа. Рационалните числа са числа, които могат да бъдат записани като дроб, p/q, където p и q са цели числа. Ние наричаме a x-координата на точката и ние наричаме b y-координата на точката
