
- Автор Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- Последно модифициран 2025-01-22 16:56.
Линейна регресия се използва за прогнозиране на стойността на непрекъсната променлива Y на базата на една или повече входни променливи за предсказване X. Целта е да се установи математическа формула между променливата на отговора (Y) и променливата на предсказателя (Xs). Можете да използвате тази формула, за да предвидите Y, когато са известни само X стойности.
По същия начин, какво е регресия в R програмирането?
Р - Линеен Регресия . Реклами. Регресия Анализът е много широко използван статистически инструмент за установяване на модел на връзката между две променливи. Една от тези променливи се нарича предикторна променлива, чиято стойност се събира чрез експерименти.
Освен по-горе, каква е добра стойност на R на квадрат? Р - на квадрат винаги е между 0 и 100%: 0% показва, че моделът не обяснява нищо от променливостта на данните за отговора около неговата средна стойност. 100% показва, че моделът обяснява цялата вариабилност на данните за отговора около неговата средна стойност.
По този начин каква е добрата стойност на R на квадрат за линейна регресия?
За същия набор от данни, по-висока Р - квадратни стойности представляват по-малки разлики между наблюдаваните данни и монтираните стойности . Р - на квадрат е процентът на вариацията на зависимата променлива, която a линеен модел обяснява. Р - на квадрат винаги е между 0 и 100%:
Как въвеждате данни в R?
Можеш въвеждане на данни като просто въведете стойности и натиснете return или tab. Можете също да използвате стрелките нагоре и надолу, за да навигирате. Когато сте готови, просто изберете Файл > Затвори. Ако въведете ls() сега трябва да видите имената на променливите, които сте създали.
Препоръчано:
Какво е съотношението Т в регресия?

Коефициентът t е оценката, разделена на стандартната грешка. При достатъчно голяма извадка, t-коефициенти, по-големи от 1,96 (в абсолютна стойност), предполагат, че вашият коефициент е статистически значимо различен от 0 при 95% ниво на доверие
Какво причинява морска регресия?
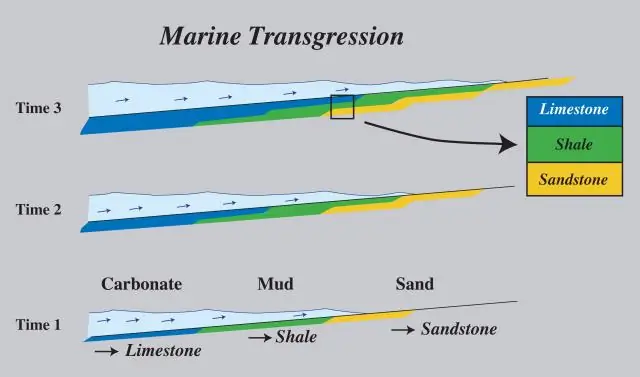
Трансгресии и регресии могат да бъдат причинени от тектонски събития като орогения, тежки климатични промени като ледникови епохи или изостатични корекции след отстраняване на натоварването от лед или седимент
Какво е спомагателна регресия?
Помощна регресия: Регресия, използвана за изчисляване на тестова статистика - като тестовата статистика за хетероскедастичност и серийна корелация или всяка друга регресия, която не оценява модела от основен интерес
За какво се използва нелинейната регресия?

Нелинейната регресия е форма на регресионен анализ, при която данните се вписват в модел и след това се изразяват като математическа функция. Нелинейната регресия използва логаритмични функции, тригонометрични функции, експоненциални функции, степенни функции, криви на Лоренц, функции на Гаус и други методи за напасване
Кога трябва да използвате корелация и кога да използвате проста линейна регресия?

Регресията се използва основно за изграждане на модели/уравнения за прогнозиране на ключов отговор, Y, от набор от променливи на предсказателя (X). Корелацията се използва основно за бързо и кратко обобщаване на посоката и силата на връзките между набор от 2 или повече числови променливи
