Видео: Как се прави конично сечение на парабола?
2024 Автор: Miles Stephen | [email protected]. Последно модифициран: 2023-12-15 23:33
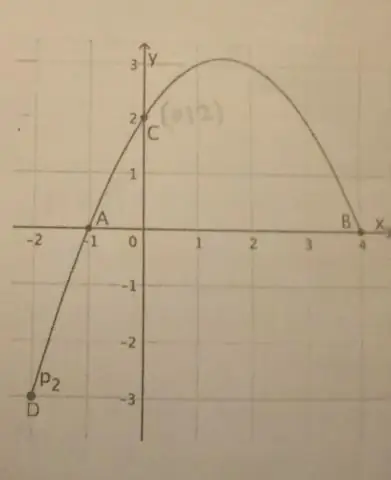
Ако парабола има вертикална ос, стандартната форма на уравнението на парабола това е: (x - h)2 = 4p(y - k), където p≠ 0. Върхът на това парабола е в (h, k). Фокусът е в (h, k + p). Директрисата е правата y = k - p.
Хората също питат, параболата конично сечение ли е?
В парабола е друг общоизвестен конично сечение . Геометричната дефиниция на a парабола е мястото на всички точки, така че да са на еднакво разстояние от точка, известна като фокус, и права линия, наречена директриса. С други думи, ексцентриситетът на a парабола е равно на 1.
Освен това, какви са 4-те вида конични сечения? Четирите конични секции са кръгове , елипси, параболи и хиперболи. Коничните сечения се изучават от доста дълго време. Кеплер за първи път забеляза, че планетите имат елиптични орбити. В зависимост от енергията на орбитално тяло са възможни орбитални форми, които са всеки от четирите типа конични сечения.
По същия начин, как се прави конично сечение?
Конични сечения се генерират от пресечната точка на равнина с конус. Ако равнината е успоредна на оста на въртене (ос y), тогава конично сечение е хипербола. Ако равнината е успоредна на генериращата права, конично сечение е парабола.
Каква е стандартната форма на парабола?
f (x) = a(x - h)2 + k, където (h, k) е върхът на парабола . FYI: Различните учебници имат различни интерпретации на препратката " стандартна форма " на квадратична функция. Някои казват, че f (x) = ax2 + bx + c е " стандартна форма ", докато други казват, че f (x) = a(x - h)2 + k е " стандартна форма ".
Препоръчано:
Какво е напречно сечение на куб?
Една точка (връх на куба) отсечка (ръб на куба) триъгълник (ако три съседни лица на куба се пресичат) успоредник (ако две двойки противоположни лица се пресичат – това включва ромб или правоъгълник) трапец (ако две двойки
Как намирате напречното сечение на квадрат?
ВИДЕО Имайки предвид това, какво е напречното сечение на квадрат? Напречни сечения . А напречно сечение е формата, която получаваме, когато режем направо през обект. В напречно сечение на този обект е триъгълник. Това е като поглед към вътрешността на нещо, направено чрез разрязване.
Как се изобразява коника на парабола?
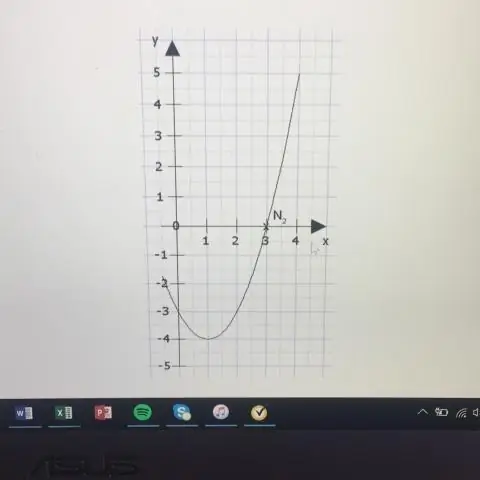
Директрисата е правата y = k - p. Оста е правата x = h. Ако p > 0, параболата се отваря нагоре, а ако p < 0, параболата се отваря надолу. Ако параболата има хоризонтална ос, стандартната форма на уравнението на параболата е следната: (y - k)2 = 4p(x - h), където p≠ 0
Как намирате върха на хоризонтална парабола?
Ако парабола има хоризонтална ос, стандартната форма на уравнението на параболата е следната: (y -k)2 = 4p(x - h), където p≠ 0. Върхът на тази парабола е в (h, k). Фокусът е в (h + p, k). Директрисата е правата x = h - p
Как намирате центъра на окръжност в конично сечение?
Стойността на r се нарича „радиус“на окръжността, а точката (h, k) се нарича „център“на окръжността. (h, k) = (0, 0), тогава уравнението се опростява до x2 + y2 = r2