Видео: Как да преобразувате обща форма в стандартна форма на хипербола?
2024 Автор: Miles Stephen | [email protected]. Последно модифициран: 2023-12-15 23:33
В стандартна форма на хипербола което се отваря настрани е (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1. За хипербола който се отваря нагоре и надолу, е (y - k)^2 / a^2 - (x- h)^2 / b^2 = 1. И в двата случая центърът на хипербола се дава от (h, k).
Освен това, каква е общата форма на хипербола?
А Общ Забележка: Стандартно Форми от Уравнение на хипербола с център (0, 0) Обърнете внимание, че върховете, ко-върховете и фокусите са свързани чрез уравнение c2=a2+b2 c 2 = a 2 + b 2.
Освен това, КАКВО Е А във формата на връх? В форма на върха на квадратен е даден от. y =a(x – h)2 + k, където (h, k) е връх . Бутото "а" в форма на върха е същото "а" като. в y =ax2 + bx + c (тоест и двете a имат абсолютно една и съща стойност). Знакът на "a" ви казва дали квадратът се отваря нагоре или се отваря надолу.
Оттук нататък каква е общата форма на елипсата?
Един общ формат на ан елипса isax2 + от2 + cx + dy + e = 0. Но толкова по-полезно форма изглежда съвсем различно: където точката (h, k) е центърът на елипса , и фокусните точки и дължините на осите на елипса може да се намери от стойностите на a и b.
Как намирате върха в стандартна форма?
Вертексна форма на квадратно уравнение -MathBitsNotebook(A1 - CCSS Math) f (x) = a(x - h)2 + k, където (h, k) е връх на параболата. FYI: Различните учебници имат различни интерпретации на препратката" стандартна форма " на квадратична функция.
Препоръчано:
Каква е стандартната форма на хипербола?
Стандартната форма на уравнението на хипербола е от вида: (x - h)^2 / a^2 - (y - k)^2 / b^2 = 1 за хоризонтална хипербола или (y - k)^2 / a^2 - (x - h)^2 / b^2 = 1 за вертикална хипербола. Центърът на хиперболата е даден от (h, k)
Как пишеш y MX B в стандартна форма?
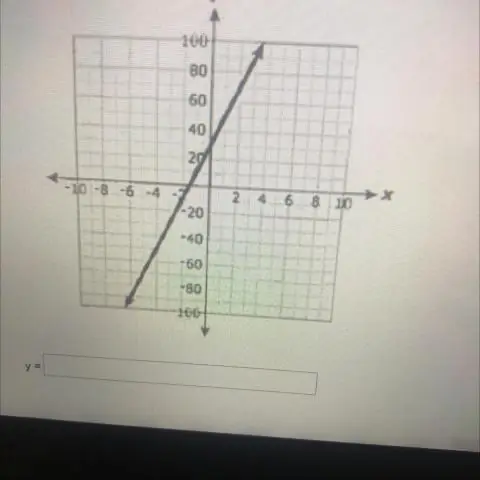
Стандартната форма на такова уравнение е Ax + By + C = 0 или Ax + By = C. Когато пренаредите това уравнение, за да получите y само по себе си от лявата страна, то приема формата y = mx +b. Това се нарича форма за отсечка на наклона, тъй като m е равно на наклона на линията, а b е стойността на y, когато x = 0, което го прави пресечена от y
Как превръщате уравнението на кръг в стандартна форма?
Стандартна форма на кръгово уравнение. Стандартната форма на уравнението на кръга е (x-h)² + (y-k)² = r², където (h,k) е центърът, а r е радиусът. За да преобразувате уравнение в стандартна форма, винаги можете да попълните квадрата отделно по x и y
Как пишете формуляр за прихващане на наклон в стандартна форма?
Стандартната форма е друг начин за писане на формуляр за пресечен наклон (за разлика от y=mx+b). Записва се като Ax+By=C. Можете също да промените формата за пресичане на наклон в стандартна форма, както следва: Y=-3/2x+3. След това изолирате y-отсечката (в този случай е 2) по следния начин: Добавете 3/2x към всяка страна на уравнението, за да получите това: 3/2x+y=3
Как преобразувате квадратно уравнение от обща форма в стандартна форма?
Всяка квадратична функция може да бъде записана в стандартната форма f(x) = a(x - h) 2 + k, където h и k са дадени чрез коефициенти a, b и c. Нека започнем с квадратичната функция в общ вид и завършим квадрата, за да го пренапишем в стандартен вид