
- Автор Miles Stephen [email protected].
- Public 2023-12-15 23:33.
- Последно модифициран 2025-06-01 05:03.
Поведението на аритметична последователност зависи от общата разлика d. Ако общата разлика d е: Положителна, то последователност ще напредване към безкрайност (+∞) Отрицателно , на последователност ще регресира към отрицателен безкрайност (−∞)
Освен това, може ли сборът от редица да бъде отрицателен?
Вие говорите за сума на безкрайно серия което предполага, че на серия е геометрична, тъй като е безкрайна аритметика серия може никога не се сближават. Имайте предвид, че общото съотношение трябва да бъде |r| < 1 за a сума да съществува. Така че, ако общото съотношение е положително там мога бъди не отрицателна сума.
Също така, каква е сумата от крайните аритметични редове? В сума на (n) условия на an аритметичен ред е (5{n}^{2}-11n) за всички стойности на (n). Определете общата разлика. В сума на аритметичен ред е (ext{100}) умножено на първия член, докато последният член е (ext{9}) умножен по първия член.
Следователно, как намирате сбора на аритметичен ред?
Да се намирам на сума на аритметика последователност, започнете с идентифициране на първото и последното число в последователността. След това съберете тези числа и разделете сума по 2. Накрая умножете това число по общия брой членове в последователността до намирам на сума.
Какво е N в серия?
Първият мандат е а1, общата разлика е d, а броят на термините е. Сборът от аритметика серия се намира чрез умножаване на броя на термините по средната стойност на първия и последния член. За да намерите, използвайте изричната формула за аритметика последователност . Решаваме 3 + (- 1)·4 = 99, за да получим = 25.
Препоръчано:
Може ли чи квадрат да бъде отрицателен?
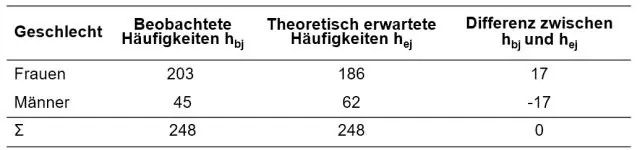
Имате предвид: Могат ли стойностите на хи квадрат да бъдат отрицателни? Отговорът е не. Стойността на хи-квадрат не може да бъде отрицателна, тъй като се основава на сбор от разликите на квадрат (между получените и очакваните резултати)
Защо Galileo ще бъде по-добър от GPS, когато бъде завършен и работи?

GPS е проектиран и използван за първи път за военно приложение. Защо Galileo ще бъде по-добър от GPS, когато бъде завършен и работи? Galileo ще превъзхожда GPS преди всичко поради прецизността на своята часовникова технология
Кое от следните трябва да бъде изпълнено, за да бъде валидна теорията за сблъсък на скоростите на реакциите?

Кое от следните трябва да бъде изпълнено, за да бъде валидна теорията за сблъсък на скоростите на реакциите? - Реагиращите молекули трябва да се сблъскат една с друга. - Молекулите трябва да се сблъскат в ориентация, която може да доведе до пренареждане на атомите. -Реагиращите молекули трябва да се сблъскат с достатъчно енергия
Как намирате сумата от краен аритметичен или геометричен ред?

Формулата за сумата от n члена на геометрична последователност се дава от Sn = a[(r^n - 1)/(r - 1)], където a е първият член, n е номерът на члена и r е общо съотношение
Кой каза, че енергията не може нито да бъде създадена, нито да бъде унищожена?

Материята не е нито създадена, нито унищожена. През 1842 г. Джулиус Робърт Майер открива Закона за запазване на енергията. В най-компактната си форма сега той нарича Първи закон на термодинамиката: енергията нито се създава, нито се унищожава
